測光システムとは何か
測光システムとは何か ―全天測光で行っている中身―
測光システムというのは、次の2つの要素をセットとして定義されるシステムである。
(1)観測ハードウェア:望遠鏡+検出器+フィルターセット (2)測光標準星:様々な明るさと分光型をもつ変光しない実在の星のセット、およびその測光システムでの等級と色指数
(注1)よくある誤解は、測光システムとはフィルターの組み合わせ(あるいは、検出器とフィルターの組み合わせ)で決まるものだ、というものである。それは不十分で、上に書いたように測光標準星とセットでやっと定義できるものである。以下の記述をじっくり読めば、その理由がわかると思います。 フィルターが波長領域を主に決定するので最重要な要素であることは確かですが、測光システム=フォルタ―システムではありません。
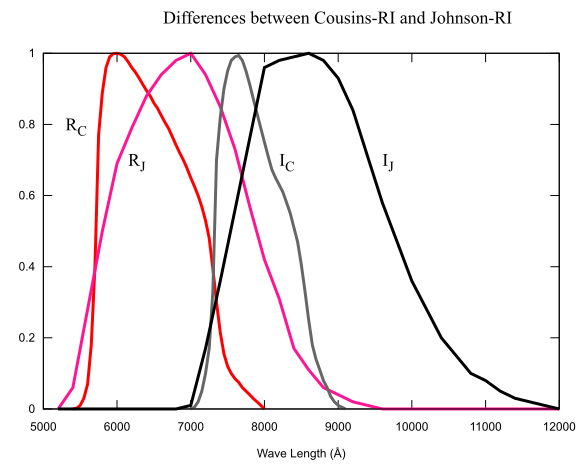
また次の図は、歴史的には最初に作られた Johnsonの UBVRIシステムのRI (R_J, I_Jと明示)と、クローン・カズンズのRcIcシステムの分光特性の違いを示したものです。R_J I_j と RcIc とは明らかに分光特性が異なっていることがわかると思います(Johnsonの方がより長波長側に位置している)。 CCDの時代になってから、単に UBVRIというとジョンソンのUBV + クローン・カズンズのRcIc システムを指すことも少なくないので、注意が必要です。 特に、例えば、 UVBRcIcのフィルターで観測しているにもかかわらず、データ処理時に UBVR_JI_Jシステムの標準星カタログを使用するなど、知らずに混同すると悲劇が起こりますので、間違ってはいけません。
(注2)全天測光とは、特に旧来の光電測光において測光システムを確立しながら目的の星の等級と色指数を測定するるために使われてきた観測方法です。Johnsonの標準UBV測光システムでは全天に10個の1次標準星と98個の2次標準星を定めて、これらの標準星で測光システムを定義している(参考文献(1))ために、調べたいある星の等級と色指数を測定する場合に、その星と全天の標準星とをできるだけ短時間で観測するので、こう呼ばれる。
なお、CCDの時代では、望遠鏡を振り回して観測する全天測光は歓迎されなくなり(望遠鏡を振り回すのは、シングルチャンネル検出器であるため)、CCDのように素子が何万個もあるようなマルチチャンネル検出器では、天頂に近いかたまった領域に標準星群を用意して、一度に多数個の標準星を観測するのが便利です。しかし、標準システムへ変換する原理は、ここで書くことと全く同じです。
(以下、「カタログ値」とは標準測光システムでのV等級と色指数のことを示す)
このページの目的:
今、標準測光システムと、それに似ているけれども少し異なるあなたの測光システムの2つがあるとして、あなたの測光システムをどのようにして標準測光システムへ変換するのか、実際の観測値を使いながら具体的手順を示します。そしてそれにより、測光システムがどのようなものなのかを理解できるようになることを目指しています。
前提とする仮定:
理解を容易にするために、本質的な測光システムの問題だけに集中できるように、以下のような理想的な環境で観測することを仮定しよう。 すなわち、
(仮定1)観測は大気外で行われる(大気減光の補正を考えなくて済む)
(仮定2)検出器には理想的なCCDカメラを用いる、つまり
*CCDの量子効率は100%である。
*ADUは1-e/countである。
*ダークノイズはゼロで、ピクセル間の感度ムラはなく、すべて
の光学系にゴミやホコリは付いていない(ダーク補正、フラット補正は不要)
*ダイナミックレンジは無限大であり、暗いところから明るいと
ころまで完璧な直線性が保証されている。
つまり、観測から得られるCCDの出力カウント数は、そのままで、CCDに入射した光子数を示していることが保証される。
(仮定3)考える測光バンドは、VとB,U の3種類とする(しかし、以下の
議論は容易に他の測光バンドへ拡張できる)
言い換えれば、すぐおわかりのように、CCD画像の処理(ダーク(Bias)、フラット処理)をきちんと行い、大気減光補正を施した後のデータそのもののことです。
設定した具体的な状況:
あなたの持つ観測ハードウェア(望遠鏡とCCDカメラ、およびUBVの3種類のフィルターセット)を使って、JohnsonのUBV標準測光システムで定義されている測光標準星のいくつかを観測した。そして、表1の左半分のような数値を得た、とします。
<表1>観測して得られたデータと標準星カタログ値
| |<------観測値-------> | <------カタログ値------>| | |||||
| 星番 | v_cnt | b_cnt | u_cnt | V | B-V | U-B |
| A | 37636 | 108143 | 49204 | 6.85 | 0.011 | -0.54 |
| F | 19143 | 55770 | 23922 | 7.59 | 0.002 | -0.55 |
| G | 16129 | 47424 | 21419 | 7.74 | -0.009 | -0.55 |
| I | 13740 | 15646 | 2063 | 7.89 | 1.028 | 0.77 |
| J | 13329 | 26254 | 7152 | 7.94 | 0.449 | -0.01 |
| N | 8686 | 5341 | 190 | 8.33 | 1.728 | 2.08 |
| O | 8433 | 7943 | 818 | 8.40 | 1.232 | 1.04 |
| P | 5733 | 15304 | 5277 | 8.89 | 0.106 | -0.27 |
| S | 3545 | 7842 | 1697 | 9.39 | 0.314 | 0.17 |
| U | 2394 | 3695 | 814 | 9.81 | 0.676 | 0.23 |
| V | 1857 | 4902 | 1267 | 10.10 | 0.122 | 0.01 |
| W | 1583 | 1420 | 109 | 10.21 | 1.292 | 1.27 |
(手順1)自然システムでの大気外での等級と色指数を求める。
用語について:自然システムまたは器械システム(英語ではnatural systemまたはInstrumental system)
あなたが使っている観測ハードウェアで得られるそのままの値のこと。バンド名の表記は小文字で表す。
vバンドでの等級 v_0 = -2.5log(vバンドでのカウント数) 色指数 (b-v)_0 = -2.5log(bバンドでのカウント数/vバンドでのカウント数) 〃 (u-b)_0 = -2.5log(uバンドでのカウント数/bバンドでのカウント数)
左辺の"_0"という表記は大気外での値を示す。 ここでは、もともと大気外で観測したという設定なので、そのままの値を使えば良いが、実際の地上観測では、大気減光の補正を施した値を使う。
<例>観測で得られた星Aのカウント数が、v,b,uバンドでそれぞれ、 37636,108143,49204カウントだとすると
V_0 = -2.5log(37636) = -11.439 (b-v)_0 = -2.5log(108143/37636) = -1.146 (u-b)_0 = -2.5log(49204/108143) = 0.855
これが自然システムでの器械等級Instrumental magnitudeと器械色指数 Instrumental Color index(indeces)である。
一方、星Aの標準UBVシステムでのカタログ値は、
V= 6.85 B-V= 0.011 U-B=-0.54
であるから、まるで異なる値となっているのがわかる。
このようにしてすべての星について計算したものを、表2の左半分に大気外等級と色指数としてまとめた。
(手順2)自然システムから標準測光システムへの変換係数を求める
この自然システムでの器械等級と器械色指数から、標準測光システムでの値へ変換するのが目的である。この手順を「自然システムから標準測光システムへの変換」という。
自然システムの量は小文字で表記する慣わしがある。大気外における自然システムの等級v_0と色指数(b-v)_0, (u-b)_0 から標準システムへの変換は次の式により行う。
V = v_0 + ε(B-V) + ζ_v (1) (B-V) = μ(b-v)_0 + ζ_bv (2) (U-B) = ψ(u-b)_0 + ζ_ub (3)
ここで、ε,μ,ψ, はそれぞれV,B-V,U-Bについての変換係数、 ζ_v,ζ_bv,ζ_ubはそれぞれV,B-V,U-Bについてのゼロ点定数と呼ばれる。
これらの係数・定数群を観測データから次の手順で得る。 まず、表2の右半分のようなカタログ値と自然システムとの差を求める。
<表2>大気外等級と色指数、およびカタログ値との差
| |<--大気外の等級と色指数---> | <----------カタログ値との差--------->| | |||||
| Name | v_0 | (b-v)_0 | (u-b)_0 | V-v_0 | (B-V)-(b-v)_0 | (U-B)-(u-b)_0 |
| A | -11.439 | -1.146 | 0.855 | 18.289 | 1.157 | -1.395 |
| F | -10.705 | -1.161 | 0.919 | 18.295 | 1.163 | -1.469 |
| G | -10.519 | -1.171 | 0.863 | 18.259 | 1.162 | -1.413 |
| I | -10.345 | -0.141 | 2.200 | 18.235 | 1.169 | -1.430 |
| J | -10.312 | -0.736 | 1.412 | 18.252 | 1.185 | -1.422 |
| N | - 9.847 | 0.528 | 3.624 | 18.177 | 1.200 | -1.544 |
| O | - 9.815 | 0.065 | 2.468 | 18.215 | 1.167 | -1.428 |
| P | - 9.396 | -1.066 | 1.156 | 18.286 | 1.172 | -1.426 |
| S | - 8.874 | -0.862 | 1.662 | 18.264 | 1.176 | -1.492 |
| U | - 8.448 | -0.471 | 1.642 | 18.258 | 1.147 | -1.412 |
| V | - 8.172 | -1.054 | 1.469 | 18.272 | 1.176 | -1.459 |
| W | - 7.999 | 0.118 | 2.791 | 18.209 | 1.174 | -1.521 |
そして変換係数を決定するために回帰分析(最小2乗フィッティング)を行う。
(i)V等級に関する変換係数とゼロ点定数の決定 (ii)B-Vに関する変換係数とゼロ点定数の決定 (iii)U-Bに関する変換係数とゼロ点定数の決定
その準備として、(1)から(3)式を変形する。
V - v_0 = ε(B-V) + ζ_v (1)'
(2)式は、両辺から(b-v)_0を引き
(B-V) - (b-v)_0 = (μ-1)(b-v)_0 + ζ_bv (2)'
また(2)式を変形して
(b-v)_0 = ((B-V) - ζ_bv)/μ
これを(2)' 式に代入し
(B-V)-(b-v)_0 = (1-1/μ)(B-V) + ζ_bv/μ (2)"
(3)式も同様にして
(U-B)-(u-b)_0 = (1-1/ψ)(U-B) + ζ_ub/ψ (3)'
これらのうち、(1)', (2)", (3)' 式を利用する。
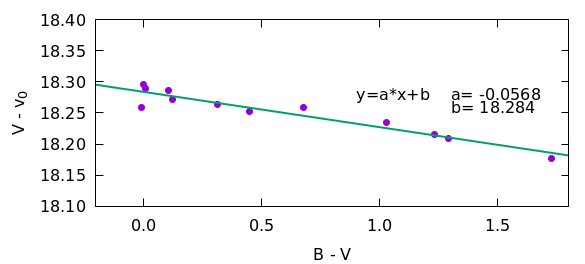
図1は、表2の右半分のうち(V - v_0)とカタログ値(B −V)の相関をグラフ化し、直線フィッティングしたものです。(1)' 式と直線の式 y-a*x+b を対比させると、この場合では、
ε= -0.0568 ζ_v = 18.284
であることがわかる。
同様に、図2は、(B-V) と (B-V)-(b-v)_0 の相関を見たもので、(2)" 式と y=a*x+b を見比べると、この例では、
1-1/μ = 0.0104 ζ_bv/μ = 1.165
であることがわかるので、結局
μ=1.011 ζ_bv=1.178
を得る。
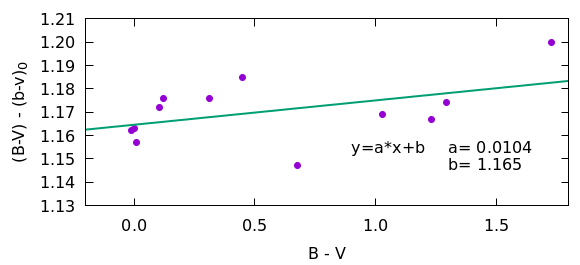
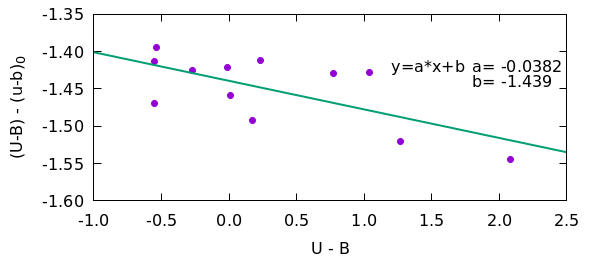
図3も、図2と同様にして、(U-B)と(U-B)-(u-b)_0の相関を見たもので、(3)' 式とy=a*x+bを見比べると、この例では、
1-1/ψ = -0.0382 ζ_ub/ψ = -1.439
であることがわかるので、結局
ψ=0.963 ζ_ub=-1.386
を得る。
こうして、式(1)から(3)は、具体的な係数を得て次のような実際の変換式群になる。実用面から(1)と(2)の順を入れ替えて
(B-V) = 1.011(b-v)_0 + 1.178
V = v_0 - 0.0568(B-V) + 18.284
(U-B) = 0.963(u-b)_0 - 1.386
(手順3)ある観測目的の星について自然システムで得た値を標準システムへ変換する
これらの変換式に、ある観測目的の星を自然システムで観測して得た値(b-v)_0, v_0,(u-b)_0を代入するだけで、標準システムでの値に変換できる。
確認のために、上で得られた変換式を使って観測値から標準システムへ変換した結果(_o)と、カタログ値との差(_o-c)を表3に示す。1回限りの観測ではこの程度の誤差が生じる。誤差を少なくするには、できるだけ観測条件の良い夜に観測する回数を増やすしかない(概ね1/√(観測回数)で誤差は少なくなる)。
<表3>観測値から標準システムに変換した等級と色指数、およびカタログ値との差
| V_o | B-V_o | U-B_o | V_o-c | B-V_o-c | U-B_o-c | |
| A | 6.846 | 0.019 | -0.563 | -0.004 | 0.008 | -0.023 |
| F | 7.579 | 0.004 | -0.501 | -0.011 | 0.002 | 0.049 |
| G | 7.765 | -0.006 | -0.555 | 0.025 | 0.003 | -0.005 |
| I | 7.998 | 1.035 | 0.733 | 0.108 | 0.007 | -0.037 |
| J | 7.997 | 0.434 | -0.026 | 0.057 | -0.015 | -0.016 |
| N | 8.534 | 1.712 | 2.104 | 0.204 | -0.016 | 0.024 |
| O | 8.540 | 1.244 | 0.991 | 0.140 | 0.012 | -0.049 |
| P | 8.894 | 0.100 | -0.273 | 0.004 | -0.006 | -0.003 |
| S | 9.427 | 0.307 | 0.215 | 0.037 | -0.007 | 0.045 |
| U | 9.876 | 0.702 | 0.195 | 0.066 | 0.026 | -0.035 |
| V | 10.118 | 0.112 | 0.029 | 0.018 | -0.010 | 0.019 |
| W | 10.359 | 1.297 | 1.302 | 0.149 | 0.005 | 0.032 |
なお、このようにして得られた変換係数は、「測光夜」と呼ばれる条件の良い夜に観測が行われた場合は、1シーズンの間はほとんど変化しない。
ここまで見てきたことをまとめると
(手順1)では、あなたの観測装置固有の目盛りにより、目的の星を含めて標準星を一緒に 絶対値を測定したことになる。 (手順2)では、カタログ値という標準測光システムのゼロ点と目盛りを使い、あなた 固有の測光システムの目盛りを較正したことになる。 (手順3)では、目的の星の等級と色指数を標準システムの目盛りで表したことになる。
なお、注意して欲しいのは、目的の星の値を測定するためには標準星の値との比は一切使っていない点である。つまり、全天測光は絶対測定であり、相対測定は行っていないということである。
参考文献
文献(1)Johnson, H. L. and Harris, D. L. 1954, ApJ 120, 196 DOI:10.1086/145903
市川隆さんの標準測光システムの解説pdfにリンクを張っておきます。今のところ、日本語で書かれた測光システムに関する最も正確で詳しい解説の一つです。
他には、
大沢清輝「星の色」(1984年、地人書館)
が参考になります。今でも中古ならAmazonで入手できます。
英語なら、次のテキストが光電測光の古典的教科書で、分かりやすい英語で、例題も具体的かつ丁寧に書かれてあります。このページの解説はこの教科書に準拠して書きました。
Astronomical Photometry A Text and Handbook for the Amateur and Professional Astronomer Arne Henden & Ronald Kaitchuck, Willmann-Bell http://www.willbell.com/photo/photo4.htm
この教科書の必要な箇所だけを訳したものもあります。
(1)整約の原理的解説
(2)整約の手引
また、JAPOA天体光電観測ガイドブックにも一通りの日本語の解説が書いてあります。
CCD測光トップへ戻る
6915
Keyword(s):[測光システム] [フィルター] [測光標準星] [システム変換]
References:[CCD測光] [標準システムへの変換]