食連星の半径

星１の半径をR1、星２の半径をR2 円軌道の半径a、軌道の位相角θとすると

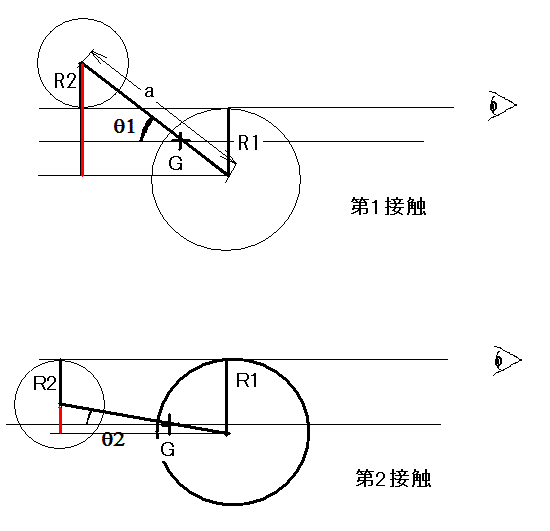
第1接触（図の上側、Gは共通重心）では 赤い線分の長さはR1+R2であり次のような関係が成り立つ

R1+R2 = a*sin(θ1)　　　‥‥（１）

同様に第2接触（図の下側）では 赤い線分の長さはR1-R2であり次式が成り立つ

R1-R2 = a*sin(θ2)　　　‥‥（２）

（１）式＋（２）式

2*R1=a(sin(θ1)+sin(θ2))

       a
 R1 = ---(sin(θ1)+sin(θ2))
       2

これを（２）式に代入して

       a
 R2 = ---(sin(θ1)-sin(θ2))
       2

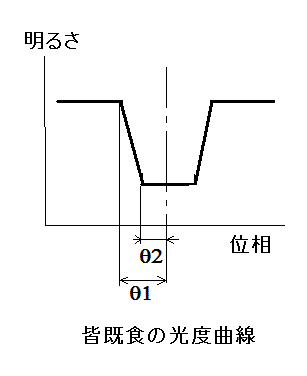
光度曲線から位相角θ1とθ2を読み取ると、軌道半径aが不明でも星の半径比R2/R1を求めることができる。

  R2      sin(θ1)-sin(θ2)
 ---- = -----------------------
  R1      sin(θ1)+sin(θ2)

OTO-Ohshima Tamashima Observatory-へ戻る

食連星の観測のページへ戻る