明るい比較星を選ぶ
結論を先に書くと
(1)比較星には、変光していない星を。 (2)比較星には、目的星と同程度の明るさか、より明るい比較星を選ぶことが大切。→(4) (3)色もまた、できるだけ目的星に似たものを。 (4)そのためには、広い望遠鏡の視野が必要
(1)もちろん、比較星が変光していることは論外なので、変光星の可能性の
ない星を選ぶことが大切である。そのためには、
- 比較星にする星が変光星でないかどうかを、変光星カタログGCVSや
ヒッパルコスデータの変光星フラグなどでチェックしておく。 それでも、変光星カタログ類には、実在するすべての変光星が網羅さ れているわけではなく、むしろ未発見の変光星の数のほうが多いかも しれないので、
- チェック星による比較星の変光性チェックは欠かせない。
チェック星(目的星と比較星に次ぐ第3の星)を同一視野に選んでおき、 観測期間を通して、比較星−チェック星の等級差が一定になっているか どうかを調べる必要がある。
- <参考>変光星カタログ
- General Catalogue of Variable Stars
- New Catalogue of Suspected Variable Stars
- <参考>変光星カタログ
国立天文台/天文学データ解析計算センター天文データセンターから入手できる。 変光星の各種カタログについてはこのURLにリストが挙げられている。
- ヒッパルコスデータ
The Hipparcos and Tycho Catalogues Search facility を利用すれば、ヒッパルコスカタログに載っている星の変光性について調べることができる。H6という項目が Coarse variability flagです。
(2)比較星は明るくなければならない
一般に行われる恒星の測光方法は、目的星と比較星の明るさの比を測定 する相対測光である。 目的星の誤差をσ_objとし、比較星の誤差をσ_compとすると、観測目的で ある等級差(=目的星の等級−比較星の等級)の持つ誤差σ_totalは、
σ_total = √(σ_obj^2+σ_comp^2)
である。 与えられた目的星の明るさは選べないので、つまりσ_objは固定されている ので、誤差を減らすために観測者に許されているのは、σ_compが最小にな るように比較星を選ぶことだけである。つまり、光子統計の教えるところにより、 目的星よりもできるだけ明るい比較星を選ぶことが大切であることがわかる。 上式を変形して
σ_total = σ_obj*√(1+σ_comp^2/σ_obj^2) = σ_obj*√[1+(σ_comp/σ_obj)^2]
一方、星が明るい時は、測光誤差はカウント数に依存すると見てよいので
σ_comp/σ_obj = √(N_comp/N_obj)
であり、また、等級の式から、
N_comp/N_obj = 10^[-0.4*(m_obj-m_comp)]
であるから、トータルの測光誤差を、目的星の測光誤差と較べると
σ_total/σ_obj =√(1+10^[-0.4*(m_obj-m_comp)])
となり、比較星の目的星に対する明るさ(暗さ)とトータルの測光誤差の 関係式を得る。それを下表とグラフに示す。
| 比較星の明るさ | トータルの測光誤差 |
|---|---|
| (目的星に対する等級差) | (目的星単独の測光誤差に対する割合) |
| -5 | 1.00 |
| -4 | 1.01 |
| -3 | 1.03 |
| -2 | 1.08 |
| -1 | 1.18 |
| 0 | 1.41 |
| 1 | 1.87 |
| 2 | 2.70 |
| 3 | 4.10 |
| 4 | 6.39 |
| 5 | 10.05 |
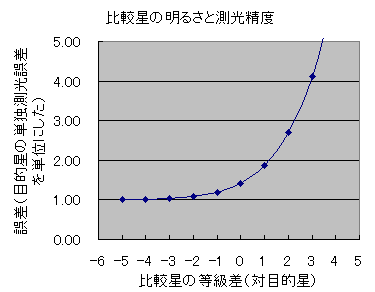
比較星が1等暗い時は、トータルの測光誤差は目的星の測光誤差の約2倍にな り3等暗い時は4倍に、と急速に増大することがわかる。 暗い比較星を選ぶことが、いかに測光精度を悪化させるかがよくわかる。
従って
比較星は、目的星と同じか、より明るいものを選ぶほど良い
しかし、現実には狭い望遠鏡の視野内で目的星より明るい星を同一視野内に 見つけることは偶然に頼るしかないし、CCDのダイナミックレンジの問題から、 極端に明るい比較星を選ぶと目的星のカウントが稼げず、逆に測光精度自体 を悪化させるので好ましくない。 このような理由から、比較的明るい星の測光では、CCDの同一視野内に明るい 比較星を確保するためには、視野が広いくなければならないことがわかる。 つまり望遠鏡の焦点距離は短いものを選ぶ必要がある。
(3)比較星は、目的星の色に似たものがよい
観測している間に星の高度は刻々と変化する。つまり星の光が通過する地球大 気の距離(厚み)が変化する。また、CCDが感度を持つ波長域では、短波長の光 は大きく減光されるが、長波長の光は減光を受けにくい(主にレーリー散乱が効く)。 つまり、目的星と比較星の色の異なる場合は、青い星は赤い星よりも大気減光の 影響を受けやすいことになる。 例えば、青い目的星と赤い比較星を選んだ場合、観測時間中に高度が共に低 くなる時には、見かけ上、目的星が比較星に較べてどんどん暗くなっていく現 象が観測される。これはある程度までは補正可能であるが、補正量というもの は少ないほど精度が高いし、そのための観測が別に必要になるので、はじめか らできるだけ色も似た比較星を選ぶ方がよい。
(4)明るい比較星の確保には、広い望遠鏡の視野が必要
(2)で見たように、明るい比較星を確保することが測光精度を上げるための必要 条件である。 そこで、比較星を選ぶために、1度四方の視野に、どの程度の星が入ってくるか を見積もってみる。全天は約4.1x10^4(以下、4.1e4とも書く)平方度である。
| 全天の星の数 | 視野1平方度 | その等級の星を | |
|---|---|---|---|
| 等級 | (理科年表) | 内に期待される | 1個見つけるのに |
| 数(個/度^2) | 必要な視野(度^2) | ||
| 6等 | 5.6e3 | 0.14 | 7.32 |
| 7等 | 1.6e4 | 0.39 | 2.56 |
| 8等 | 4.3e4 | 1.0 | 0.95 |
| 9等 | 1.2e5 | 2.9 | 0.34 |
| 10等 | 3.5e5 | 8.5 | 0.12 |
| 11等 | 8.7e5 | 21 | 0.05 |
上記の値は、多くの星が集中している天の川の領域を含んだものである。 理科年表によれば、天の川から20度ほど離れると、星の数は約1/2になる。 さらに、比較星には変光星でなく色も似ている星を選ぶ必要性も考慮すると 1度四方の視野を持った光学系では、9等から10等の適した比較星が 1個見つかると考えてよいだろう。
焦点距離500mmの望遠鏡に、実サイズ10mmx10mmのCCD(例えばST-9)をつけると (10/500)*180/3.14=1.14度四方の視野が得られる。
結論: 視野は1度四方は確保したい 10mm*10mmのCCDカメラを使用する場合は、焦点距離500mmを目安にすると良い。
端的に書くと、
望遠鏡の焦点距離は短く、 CCDの面積は広く
(5)追加:視野が狭い望遠鏡の救いの神 アンサンブル測光
最近では、同一視野内に目的星と同程度の明るさの比較星が得られない場合に アンサンブル測光が行われることが多くなった。 これは、同一視野内の複数の星を比較星として測光し、そのカウント数を足し合わせて 一つの仮想比較星のカウント数として、目的星と比較測光する方法である。
この方法は、明るい比較星が同一視野内にとれない場合、救いの神となる。 また、比較星の色の違いを平均化するし、もしその中に変光星が含まれていても (もちろん事前にそんな星は除くべきである)、影響は少なくなる
なお、複数の比較星として選ぶ星は、できれば目的星を取り囲む配置にした方が 大気差やその他の誤差をより少なくする。
後述する測光ソフトAIP4WinではVer.2から、32個までの比較星(C1からC32))を選べ、 こま毎に望遠鏡の追尾がずれても自動トラッキングモードで測光してくれて、最後に "V-C1"以外に"V-Ens"の値もレポートしてくれる。
CCD測光トップへ戻る
4653
Keyword(s):
References:[CCD測光]