フラックスを振動数から波長へ変換する場合
星のスペクトルの理論曲線(例えばここを見る)と 横軸は波長なのに、縦軸はF_ν(←vに見えるがニュー、以下同じ)になっている。 グラフの形を見るだけならこれでもよいが、測光と結びつけようとすると数値的に厳密でなければならないので、縦軸をF_λに直す必要が出てくる。
ここで、波長λと振動数νの関係を考える。 光の波の公式は
C=νλ
である。 Cは光速(=定数)であるから、波長λと振動数νの積が一定、 つまりは波長λと振動数νは反比例していることになる。
グラフに示すと、下図左側のような双曲線グラフになる。
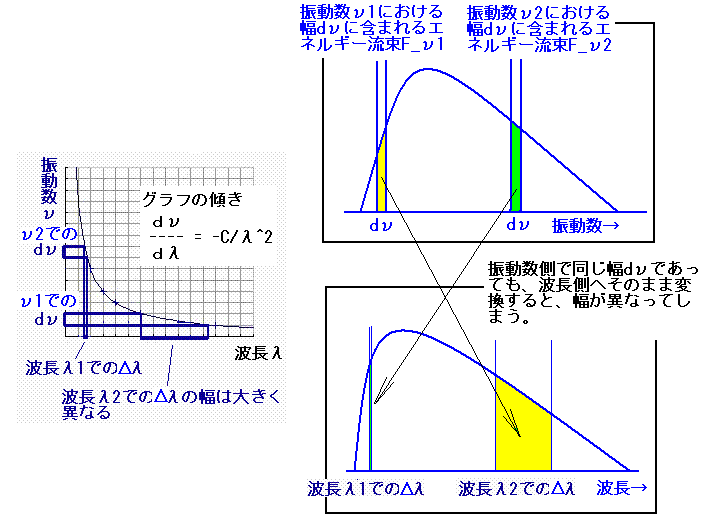
反比例グラフの傾きは波長(横軸の座標)によって異なるために、振動数から波長へ変換する際に、振動数の側で同じdν(単位振動数=1Hz)という幅であっても、そのまま波長に変換したのでは、波長によって異なる幅になる。
欲しいのは、波長によらず同じ幅dλ(単位波長=1Å)あたりに含まれるエネルギー流束であるから、これではまずいことになる。(上図右)
それを補正するために、 F_νからF_λに直す場合には
F_λ= F_ν*|dν/dλ|
で変換する必要がある。F_νに掛けるべきdν/dλは次で得られる。
ν=C/λ の両辺をλで微分すると
dν/dλ=-C/λ^2
であるので、 従って、
F_λ= F_ν*C/λ^2
で計算すればよい。
5969
Keyword(s):[フラックス] [振動数] [波長]
References:[天体の分光]